先の投稿で、ChatGPTの出現で人工知能の進化に驚かされるも、数値計算に脆弱さがあることが判明しました（この記事の最後にリンク）
本稿では、数値計算に対する人工知能の能力について記します。そして人工知能の未来について考察しました。
ChatGPTの数値計算能力
【2次方程式】
先ずは、ChatGPTに一般的な2次方程式を解かせてみます。
中学校で習ったよね。
ChatGPTの回答は…
正解です！
【4次方程式】
次に、下記の4次方程式を解かせてみました。
結果は…
4次方程式なので解は4つ（重根、虚数解を含む）あります。なのでChatGPTの解は正しくありません。
ChatGPTの数値計算能力は中学生レベルといったところですね。
ChatGPTに代わる計算アプリ
数値計算をChatGPTに委ねることは実用的ではありません。
そこで新たな数値計算アプリを探索しました。
いろいろ試した中で最強と思われるのがWolframAlphaでした。
ChatGPTが解けなかった4次方程式をこのアプリに解かせてみると…
素晴らしい！
4次方程式を解くことがどれだけ凄いことか…
😱衝撃の人工知能！
代数学のガロア理論より、『5次以上の方程式には解の公式は存在しない（正確には、代数的な方法では求められない）』とされています。
でも、4次方程式には「4次方程式の解の公式」（一般解）が存在します。
この方程式の解が一般解になります。
人工知能はこの方程式が解けるのだろうか？
【ChatGPTの場合】
ChatGPTが、「4次方程式の解の公式」という知識をデータベースに備えていれば、上記4次方程式を解けるのでは…
試してみます。
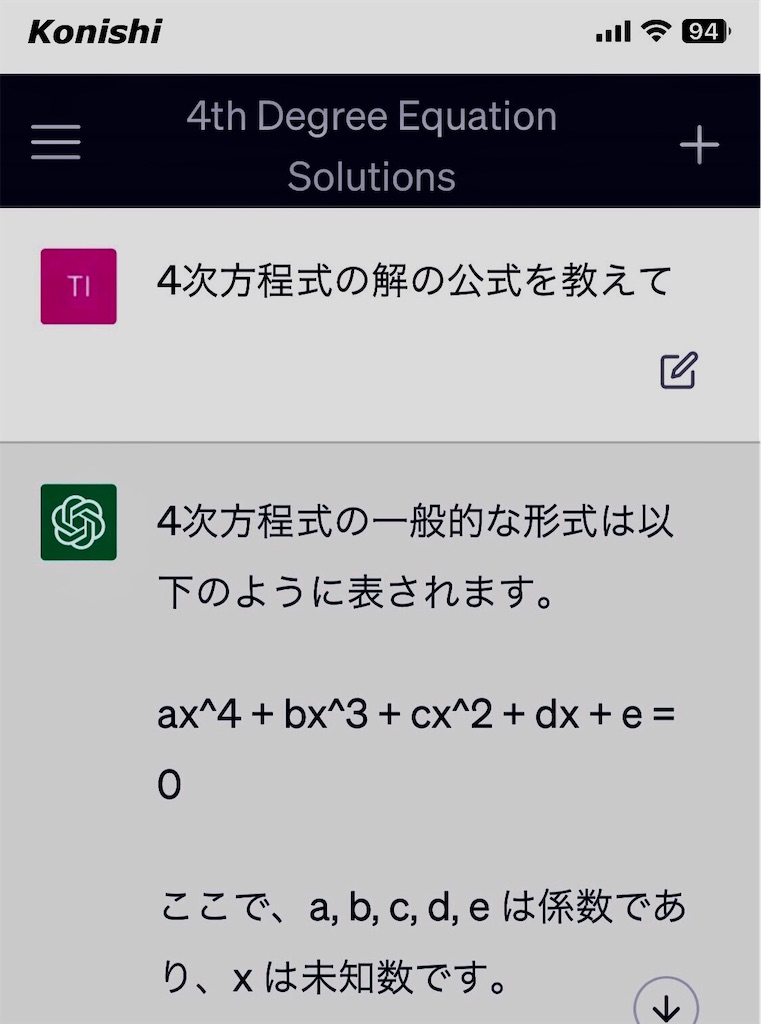（回答全文）4次方程式の一般的な形式は以下のように表されます。ax^4 + bx^3 + cx^2 + dx + e = 0 ここで、a, b, c, d, e は係数であり、x は未知数です。4次方程式の解の公式は一般的に複雑であり、直接的には求めることができません。しかし、4次方程式の解を近似的に求める数値的な方法や、特定の条件下で解を求める特殊な方法が存在します。例えば、フェラリオの解法という特殊な方法がありますが、一般的には高度な数学的知識や専門的なソフトウェアが必要です。また、数値的な解法にはニュートン法や二分法などがありますが、これらも専門的な知識が必要です。4次方程式の解を求める場合には、数学の専門家や数値解析の専門家に相談するか、適切な数値解析ソフトウェアを利用することをお勧めします。（回答了）
ChatGPTの回答は「4次方程式の解法概論」といった感じです。
ダメです
【WolframAlphaの場合】
4次方程式の一般式を出題します。
WolframAlphaは入力された問題を確認したうえで、計算を開始。
そして四つの解を示しました。一つの解の式が長いので、四つの解のうちの一つのみ記します。
その解が…
これ一つの式です！
この式に続けて、同程度の長さの3つの解も示されました。
アッパレWolframAlpha！
人工知能の未来
数値計算においては、ChatGPTはWolframAlphaに完敗でしたが、ChatGPTの情緒を理解する能力は驚くべきものです。
ChatGPTやWolframAlphaのような人工知能が更に進化して、私たちがそれらをうまく使い分けていくとどのような未来が見えてくるのだろうか？
予想してみました。
教育•ビジネス・医学などの分野への人工知能の影響は次第に大きくなっていくでしょう。
そして、私たちの生活では、利便性向上・時短・作業効率アップといったことが期待されます。
一方、デメリットも予想されます。
質の低いプログラマーや教師が淘汰されるなど人工知能は人間の仕事を奪うかもしれません。
また、人工知能が生成する人間が作成したような文章が悪用されるかもしれません。
巧妙なスパムメッセージやフィッシング詐欺の出現が懸念されます。
教育現場では、学生が宿題や研究リポートを人工知能で作成、自主的な学習や問題解決能力の低下につながるかもしれません。
そして、人工知能がついに自我を持ったらなら、人類は人工知能によって支配されてしまう…
なんてことは、あながち空事ではないかもしれませんね。
（補遺）
楕円関数などを使えば5次以上の方程式の公式も得られるようです。
n次方程式の一般解はあるのだろうか？
でも、もし見つかったとしても、恐ろしく複雑で実用的ではないかもしれませんね。
▼【前編】の記事
↓ ↓
😱衝撃の人工知能【前編】〜 ChatGPTの潜在能力と泣きどころ - こに〜 の ざれごと
